On 2015-06-11, I defended my PhD thesis entitled "Multiresolution classification using combination of density estimators" in the Systems Research Inistitute of the Polish Academy of Sciences.
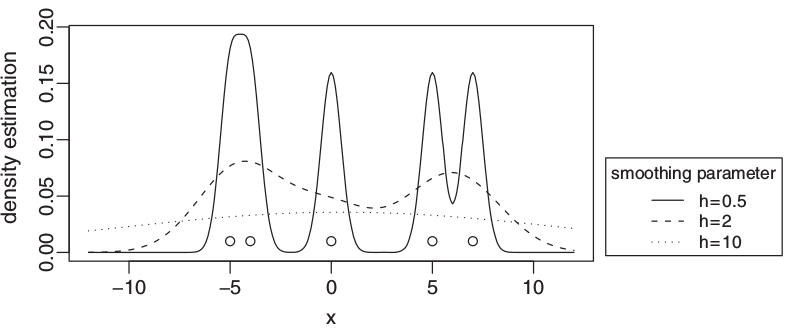
In the thesis, we introduce a classification algorithm based on an idea of "multiple-resolution" (or "multiscale") approach to data analysis. In practice, the method uses an average of kernel density estimators where each estimator corresponds to a different data "resolution" (see the figure above for estimation of density generated by kernel density estimators with different smoothing parameters which can be interpreted as a multiple-resolution view of given five data points). First, we examine theoretical properties of this method; next, we propose a practical implementation of such algorithm with parameters of the density estimators and their number adjusted to minimize the misclassification probability. Subsequently, we test the algorithm on artificial data sets characterized by a multiple-resolution property. The tests show that the introduced algorithm is superior to the basic version based on one estimator per class. We also test the algorithm on benchmark data sets and compare the results obtained with the results of the basic version and other popular classification algorithms. The method is shown to fare better than the basic version and to be on a par with other popular algorithms.
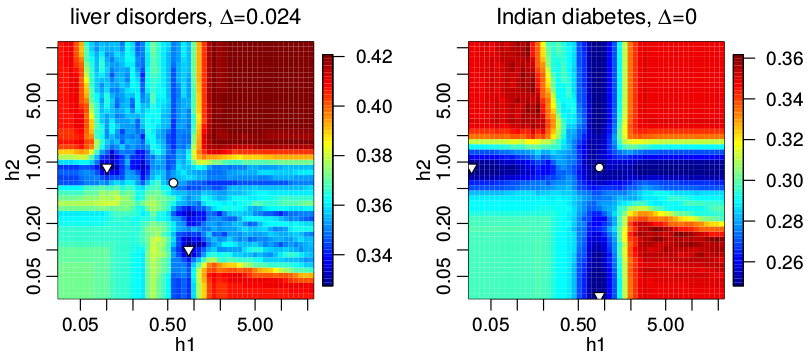
The image above is an intuitive data-based justification of why the proposed algorithm using many kernel density estimators is better for certain data sets than the basic version of the method using a single density estimator per class. The image shows the mean classification error computed for two benchmark data sets: BUPA liver disorders and Pima Indians diabetes. Two density estimators per class with the same value of smoothing parameter per class were used. The more more the color of the point resembles blue, the smaller the value of given function in this point. The global minima of the function lying outside of the diagonal are marked with triangles while the minimum for points lying on the diagonal is marked with a circle. The basic version of the method can achieve only the values lying on the diagonal; however, the proposed algorithm can achieve all shown values. The value next to the ∆ symbol above the plots is the difference between the minimal value of the function for points lying on the diagonal and the value of the global minimum. One can see that in case of the BUPA liver disorders dataset, the difference is nonzero thus we can expect a smaller classification error when applying the proposed algorithm. In case of the Pima Indians diabetes the difference is zero, so no gain is expected.
The thesis is mainly an extension of paper M. Kobos, J. Mańdziuk. Multiple-resolution classification with combination of density estimators. Connection Science, 23(4):219–237, 2011.